（用C语言编程实现）
一、实验目的
1、理解最速下降法的求解原理和程序框图；
2、理解C语言程序的基本结构，根据程序框图运用C语言编写正确的程序；
3、掌握在Microsoft Visual C++环境下C语言程序的上机调试过程。
二、实验前准备
1. 复习Microsoft VisualC++ 6.0开发环境的使用方法。
2. 复习教材相关内容。
3. 写出程序清单。
三、实验条件
1）硬件：具有良好配置的电脑；
2）软件：Microsoft Visual C++ 6.0.
四、实验内容和步骤
1.最速下降法的程序框图
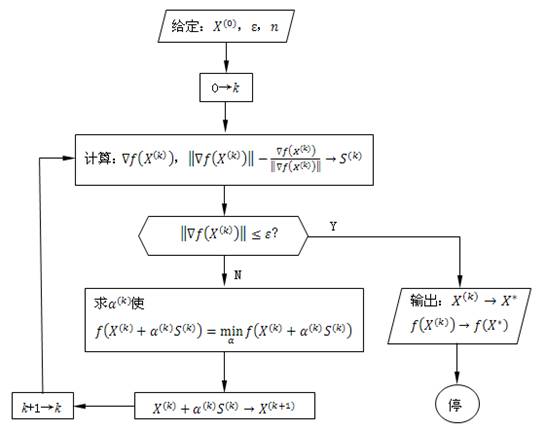
图1.1 最速下降法程序框图
2. 实验任务和程序代码
（1）任务
已知目标函数
，初始点
,迭代精度
，试用最速下降法（亦称牛顿法、梯度法）目标函数的极小点和极小值。
解：运用梯度法可求出此函数的最优步长
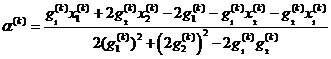
其中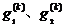
分别为目标函数在
处的梯度向量。
，
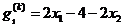（2）C语言代码
#include <stdio.h>
#include <math.h>
#define EP 0.001
float H,s[2];
float x[2]={1,1};
float f(float *q)
{
float p;
p=pow(q[0],2)+2*pow(q[1],2)-4*q[0]-2*q[0]*q[1];
return(p);
}
float h()
{
floathh;
hh=(x[0]*s[0]+2*x[1]*s[1]-2*s[0]-s[1]*x[0]-s[0]*x[1])/(pow(s[0],2)+2*pow(s[1],2)-2*s[0]*s[1]);
/* 求最佳步长*/
return(hh);
}
main()
{
floaty,R;
int i=0,n=0;
do
{
n=n+1;
s[0]=2*x[0]-4-2*x[1];
s[1]=4*x[1]-2*x[0];
R=sqrt(pow(s[0],2)+pow(s[1],2));
printf("\n R is %f.",R);
H=h();
for(i=0;i<=1;i++)
x[i]=x[i]-H*s[i];
}
while(R>EP);
y=f(x);
printf("\n The Min is %f.",y);
for(i=0;i<=1;i++)
printf("\n The X%d is %f.",i,x[i]);
printf("\n The Number is %d.",n);
}
3.上机操作步骤
3.1 创建工程
（1）启动 Microsoft Visual C++ 6.0
启动VC6.0可以通过“开始”菜单，也可以通过桌面快捷方式等方式。
图1.2 VC6.0开发环境
启动之后，我们看到的是空白的VC6.0开发环境截图如图1.2所示。跟大多数的Windows 应用程序一样，VC6.0最上面是菜单，然后是工具栏，中央是工作区，最下面一行是状态栏。我们现在看到的工作区，左边是Workspace 窗口，右边是灰底的空白窗口。
（2）创建一个工程
在VC6.0中，一个源程序文件必须属于一个工程（Project）；所以我们首先来创建一个工程，做如下操作。
选择菜单：文件à新建...
打开下面窗口如下图1.3所示。
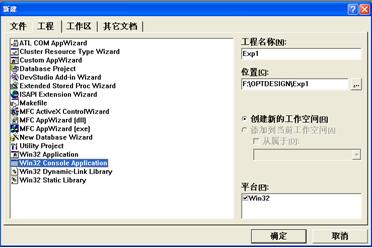
图1.3 创建工程界面
选择“Win32 Console Application”，也就是Windows 32位控制台程序（也称“黑屏”程序）。输入工程名称，指定工程存储位置，点击“确定”按钮，弹出如图1.4所示的Win32控制台应用程序配置界面，选择第一个选项，也就是默认选项：一个空的工程，然后点击完成按钮。创建一个空的工程。
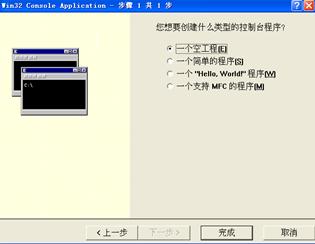
图1.4 Win32控制台应用程序配置界面
（3）确认创建新工程
如下图1.5窗口显示出之前所做的配置，以供最后检查。如果确认无误，该项目将被创建。
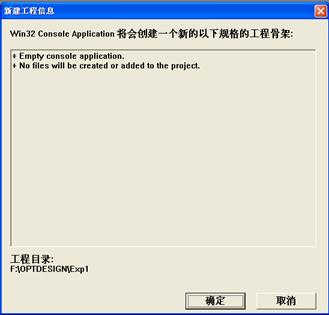
图1.5 新项目信息窗口
确认该页面显示的内容都是正确的后，点击：确定按钮，创建该项目。VC6.0会根据所填写的配置创建相关的文件夹，创建完成后会显示创建的结果，如下图1.6所示。
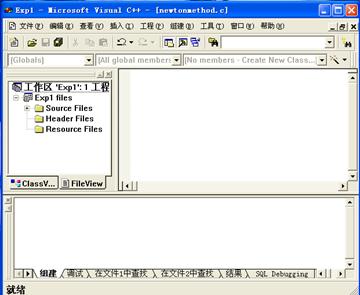
图1.6 项目创建后VC6.0界面
在窗口的左半部分的Workspace上，我们可以看到有两个，ClassView和FileView。ClassView页面会显示当前工程中所声明的类、全局变量等；对于编写C语言程序来说，这个页面没有什么大的作用。FileView页面显示了三个预定义的逻辑文件夹：“Source Files”、“Header Files”、“ResourceFiles”。
3.2 添加一个文件到一个空的工程中
上一节中创建了一个空的工程，本节将添加一个源代码程序到该工程中。
（1）创建新的.C源文件
选择菜单：文件 -->新建... ，打开下面窗口，如下图1.7所示。
图1.7
在Files 标签页面中，进行操作如下表2.1所示。
表2.1创建.C源文件操作
顺序 |
选项 |
操作 |
说明 |
1 |
文件类型 |
选择“C++ Source File” |
因为这里没有 C Source File 选项，所以我们选择 C++ 语言的对应项。 |
2 |
文件名 |
输入：newtonmethod.c |
注意：newtonmethod.c后面的“.c”后缀是必要的。如果是要创建.cpp件，该后缀就可以不写了。 |
3 |
位置 |
保持默认值，不需要修改。 |
|
4 |
完成 |
点击＂OK＂按钮 |
|
（2）查看源文件
当该.c源文件创建后，在左边Workspace 窗口中的FileView标签页面中，可以看到该新创建的newtonmethod.c节点，如图1.8所示。
图1.8 创建源文件newtonmethod.c后的界面
编写程序
（1）编写源代码
在程序编辑窗口输入C语言代码，编写完成后的结果如图1.9所示。
图1.9 编写程序界面
（2）编译连接和运行源程序
①点击工具栏中的“编译”工具
，这时系统开始对当前的源程序进行编译。如果编译完全成功，会显示“newtonmethod.obj- 0 error(s), 0 warning(s)”。另外，即便有一些warning，也可能编译成功。如果编译未成功，将所发现的错误显示在屏幕下方的“组建”窗口中。根据错误提示，修改程序后再重新编译，如还有错误，再继续修改、编译，直到没有错误为止。编译后的状态栏显示如图1.10所示。
图1.10 编译后的界面
②.编译无误后，点击工具栏中的
进行连接，这时，在屏幕下方的“组建”窗口中会显示如下信息：“exp1.exe- 0 error(s), 0 warning(s)”，说明编译连接成功，如图1.11所示，并生成以源文件名为名字的可执行文件（exp1.exe）。
图1.11 连接后的界面
③.运行程序，选择“组建”菜单中的“! 执行[exp1.exe]”选项。这时，会出现一个“MS-DOS”窗口，输出结果显示在该窗口中（如图1.12所示）。
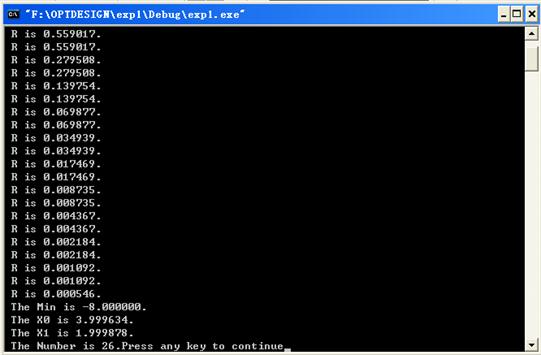
图1.12 执行结果
到此，得到目标函数的极小点为
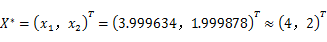
极小值为-8。
④.运行结束后，可以回到“文件”菜单，点击“关闭工作空间”选项，关闭当前文件窗口。
五、实验报告
试用最速下降法求目标函数
的极小点和极小值。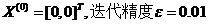
。
实验二基于MATLAB优化工具箱的优化计算（一）
一. 实验目的
1.了解利用MATLAB优化工具箱进行优化计算和设计的一般步骤；
2.了解MATLAB优化工具箱常用的优化功能函数和适用场合；
3.会运用ATLAB优化工具箱进行优化计算和设计。
二. 实验条件
1.软件：MATLAB 7.0
2.硬件：配置良好的计算机
三. 实验相关知识
1.运用MATLAB工具箱进行优化计算和设计的一般步骤
（1）针对具体工程问题建立优化设计的数学模型，模型中应将不等式约束条件表示成g(X)≤0的形式；
（2）建立目标函数文件（M文件），文件的内容主要为描述目标函数的表达式等，并将文件以自定义的目标函数文件名存储在文件夹中；
（3）建立约束函数文件，约束文件中不等式约束函数式均以≤0的形式表达，以自定义的约束函数文件名存储在文件夹中；
（4）建立调用优化工具函数的命令文件，文件内容包括初始点、设计变量的边界约束条件、运算结果输出等内容，以自定义的命令文件名存储于文件夹中。
（5）将优化设计的命令文件复制到MATLAB命令窗口中进行运算求解。
2.MATLAB优化工具箱常用的优化功能函数
求解线性规划问题的主要函数是linprog。
求解二次规划问题的主要函数是quadprog。
求解无约束非线性规划问题的主要函数是fminbnd、fminunc和fminsearch。
求解约束非线性规划问题的主要函数是fgoalattain和fminimax。
四. 实验内容
（一）线性规划问题的优化求解
1.线性规划的数学模型
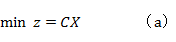
s.t.
式（3.1）
上式中：
式（a）为线性目标函数，式（b）为线性不等式约束，式（c）为线性等式约束，式（d）为设计（决策）变量的边界条件。
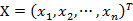，为各个决策变量构成的列向量；
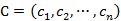，为目标函数各维变量的系数向量；
A——不等式约束方程的系数矩阵；
——等式约束方程的系数矩阵；
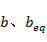——分别为不等式约束方程和等式约束方程右端的常数；
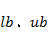——分别为决策变量的下限和上限；
2.MATLAB中函数调用格式
函数名：linprog
格式：
x=linprog(C，A，b)求解问题min C*X，约束条件为A*X≤b。
x=linprog(C,A,b,Aeq,beq)求解上面的问题，但增加等式约束，即Aeq*X=beq，若没有不等式存在，则令A=[]、b=[]。
x =linprog(C,A,b,Aeq,beq,lb,ub)定义设计变量x的下界lb和上界ub，使得x始终在该范围内，若没有等式约束，令Aeq=[]、beq=[]。
x = linprog(C,A,b,Aeq,beq,lb,ub,x0)设置初值为x0，该选项只适用于中型问题，默认时大型算法将忽略此值。
x =linprog(C,A,b,Aeq,beq,lb,ub,x0,options)用options指定的优化参数进行最小化。
[x,fval]= linprog(...)返回解x处的目标函数值fval。
[x,fval,exitflag]= linprog(...)返回exitflag值，描述函数计算的退出条件。
[x,fval,exitflag,output]= linprog(...)返回包含优化信息的输出变量output。
[x,fval,exitflag,output,lambda]= linprog(...)将解x处的拉格朗日乘子返回到lambda参数中。
参数说明：
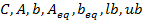等参数已在前面数学模型的形式中作了说明。
x——最优解；
——返回目标函数在最优点x点的函数值，即最优值；
exitflag——返回算法的终止标志。
exitflag>0，表示函数收敛于解x；
exitflag=0表示超过函数估值或迭代的最大数字；
exitflag<0表示函数不收敛于解x；
output——返回优化算法信息的一个数据结构。
output=iterations表示迭代次数；
output=algorithm表示使用的运算规则；
output=icgiterations表示PCG跌打次数。
lambda——解x的Lagrange乘子，它有以下属性：
lambda=lower,表示下界lb；
lambda=upper表示上界ub；
lambda=ineqlin表示不等式约束；
lambda=eqlin表示等式约束。
x0——初始点；
options——可选项；
需要说明的是，由于MATLAB中函数调用格式默认求解线性规划的极小值，因此如果要求线性规划的最大值，需要将线性规划转换为求最小值的形式。
3.应用举例
【例1】（生产规划问题）：某厂利用A、B、C三种原料生产甲、乙、丙三种产品，已知生产每种产品在消耗原料方面的各项指标和单位产品的利润，以及可利用的数量，试制定适当的生产规划使得该工厂的总利润最大。
单位产品所消耗的原料
产品 原料 |
甲 |
乙 |
丙 |
现有原料数量（千克） |
A |
3 |
4 |
2 |
600 |
B |
2 |
1 |
2 |
400 |
C |
1 |
3 |
2 |
800 |
单位产品利润（万元） |
2 |
4 |
3 |
合计：1800千克 |
解：（1）确定决策变量：
设生产甲、乙、丙三种产品的数量分别是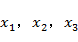
，
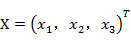
（2）建立目标函数：
根据三种单位产品的利润情况，按照实现总的利润最大化，建立关于决策变量的函数：
（3）确定约束条件：
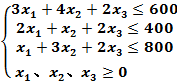
（4）在MATLAB命令窗口中依次输入下列系数：
>> C=[-2,-4,-3];
>> A=[3,4,2;2,1,2;1,3,2];
>> b=[600,400,800]';
>>Aeq=[];
>>beq=[];
>>lb=zeros(3,1);
（5）调用linprog函数
>> [x,fval]=linprog(C,A,b,Aeq,beq,lb)
得到如下的最优结果：
Optimizationterminated.
x =
0.0000
66.6667
166.6667
fval=
-766.6667
（二）无约束非线性规划问题
无约束非线性规划问题的MATLAB函数有fminbnd、fminsearch和fminunc三类，它们的适用范围见图3.1所示。
图3.1无约束非线性规划问题的三类函数
1.有边界非线性最小化函数——fminbnd
（1）功能和格式
功能：找到固定区间函数的最小值。
使用格式：
[x,fval]=fminbnd(fun，x1，x2，options)
x——返回目标函数的最优解
fval——返回目标函数的最优值
fun——目标函数
——设置优化变量给定区间的上下界；
options——设置优化选项参数
（2）应用示例
【例2】求解一维无约束优化问题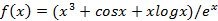
在区间[0,1]中的极小值。
解：首先编制求解优化问题的M文件。
点击Matlab菜单栏File--»New--»M-File，打开M文件编辑器窗口，按图3.2的格式编辑M文件。
图3.2 M文件
并将文件命名为fun。
然后在命令窗口输入：[x,fval]=fminbnd(@fun,0,1)，即可得到以下运行结果。
图3.3运行结果
为了显示函数图形，我们还可以在命令窗口依次输入ezplot(@fun,[0,10])、title('(x^3+cosx+xlogx)/e^x')、grid on，将得到如图3.4所示的函数图形。
图3.4函数图形
2.fminsearch函数
（1）功能及格式
功能：求多变量函数的最小值。
格式：
x =fminsearch(fun,x0)
x =fminsearch(fun,x0,options)
[x,fval]= fminsearch(...)
[x,fval,exitflag]= fminsearch(...)
[x,fval,exitflag,output]= fminsearch(...)
说明：
fun——目标函数；
options——设置优化选项参数；
x——返回目标函数的最优解；
fval——返回目标函数在最优解x点的函数值；
exitflag——返回算法的终止标志；
output——返回优化算法的信息的一个数据结构。
（2）应用示例
【例3】求函数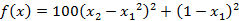
的极小值，初始点x0=[-1.2,1]。
解：首先编制求解优化问题的M文件。M文件内容和格式如图3.5所示。
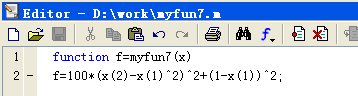
图3.5 M文件
然后在命令窗口输入：[x,fval] =fminsearch(@myfun7,[-1.2, 1]),按回车键，即可得到如下运行结果：
x =
1.0000 1.0000
fval =
8.1777e-010
这跟理论计算结果“x=[1,1]，最优值为0”极为相近。
小提示：当需要清除MATLAB命令窗口里的内容时，输入clc命令即可。
3.fminunc 函数
（1）功能和格式
功能：找到无约束多变量函数的最小值。
格式：
x =fminunc(fun,x0)
x =fminunc(fun,x0,options)
[x,fval]= fminunc(...)
[x,fval,exitflag]= fminunc(...)
[x,fval,exitflag,output]= fminunc(...)
[x,fval,exitflag,output,grad]= fminunc(...)
[x,fval,exitflag,output,grad,hessian]= fminunc(...)
grad是返回目标函数在最优解x点的梯度；
hessian是返回目标函数在最优解x点的 hessian矩阵值。
其余参数的意义跟前面相同，在此不再累赘述。
（2）应用示例
【例4】求函数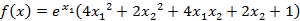
的最小值，初始点x0=
[-1,1]。
解：首先，编写m文件，格式和内容如图3.6所示。
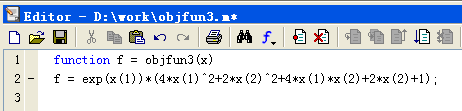
图3.6 M文件
然后在MATLAB命令窗口输入：
x0 =[-1,1]; % Starting guess
options =optimset('LargeScale','off');
[x,fval,exitflag,output]= fminunc(@objfun3,x0,options)，按回车键，即可得到如下运行结果：
Optimizationterminated: relative infinity-norm of gradient less than options.TolFun.
x =
0.5000 -1.0000
fval =
1.0983e-015
exitflag =
1
output =
iterations: 8
funcCount: 66
stepsize: 1
firstorderopt:7.3704e-008
algorithm:'medium-scale: Quasi-Newton line search'
message:'Optimization terminated: relative infinity-norm of gradient less thanoptions.TolFun.'
【例5】求函数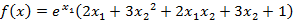
的最小值，初始点x0=[0,0]。
解：Matlab程序为：
fun='exp(x(1))*(2*x(1)^2+3*x(2)^2+2*x(1)*x(2)+3*x(2)+1)';
x0=[0,0];
options=optimset('largescale','off','display','iter','tolx',1e-8,'tolfun',1e-8);
[x,fval,exitflag,output,grad,hessian]=fminunc(fun,x0,options)
运行结果为：
Gradient's
Iteration Func-count f(x) Step-size infinity-norm
0 3 1 3
1 9 0.369485 0.135362 0.813
2 12 0.284572 1 0.77
3 18 0.134248 0.424466 0.137
4 21 0.133024 1 0.018
5 24 0.132968 1 0.00839
6 27 0.132961 1 0.000935
7 30 0.132961 1 5.28e-005
8 33 0.132961 1 1.1e-006
9 36 0.132961 1 3.91e-008
Optimizationterminated: relative infinity-norm of gradient less than options.TolFun.
Computingfinite-difference Hessian using user-supplied objective function.
x =
0.2695 -0.5898
fval =
0.1330
exitflag =
1
output =
iterations: 9
funcCount: 36
stepsize: 1
firstorderopt:3.9116e-008
algorithm:'medium-scale: Quasi-Newton line search'
message:'Optimization terminated: relative infinity-norm of gradient less thanoptions.TolFun.'
grad =
1.0e-007*
-0.0186
-0.3912
hessian =
5.1064 2.6186
2.6186 7.8561
本例的程序对参数options进行了设置。
'largescale','off'，关闭了大规模方式；
'display',用来控制计算过程的显示；
'iter'表示显示优化过程的每次计算结果；
'off'表示不显示所有输出，'final'仅输出最后结果；
'tolx'用来控制输入变量x的允许误差精度，本利设置为1e-8；
'tolfun'是控制目标函数的允许误差精度，缺省值是1e-4，本例为1e-8。
实验三 基于MATLAB优化工具箱的优化计算（二）
一. 实验目的
1.了解MATLAB求解非线性约束优化问题的fmincon函数形式；
2.会运用fmincon优化工具箱进行优化计算和设计。
二. 实验条件
1.软件：MATLAB 7.0
2.硬件：配置良好的计算机
三、实验内容
1、MATLAB求解非线性约束优化问题的fmincon函数格式和语法说明
fmincon是求解多维约束优化问题
minf(X)
s.t.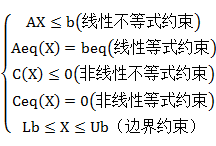
的优化工具箱函数，它的语法说明如下：
[x,fval,exitflag,output,grad,hessian]=
fmincon(@fun,x0,A,b,Aeq,beq,Lb,Ub,‘Nlc’,options,P1,P2…)
其中，输出参数有：
x是返回目标函数的最优解；
fval是返回目标函数在最优解x点的函数值；
exitflag是返回算法的终止标志；
output是返回优化算法的信息的一个数据结构；
grad是返回目标函数在最优解x点的梯度；
hessian是返回目标函数在最优解x点的hessian矩阵值。
输入参数有：
fun是调用目标函数的函数文件名；
x0是初始点；
A和b分别是线性不等式约束条件的系数矩阵和常数向量；
Aeq和beq分别为线性等式约束条件的系数矩阵和常数向量；
Lb和Ub为设计变量X的下界向量和上界向量；
‘Nlc’是定义非线性约束条件的函数名；
options是设置优化选项参数；
P1,P2等是传递给fun的附加参数.
参数A,b,Aeq,beq,Lb,Ub,options如果没有定义可用空矩阵符号“[]”代替。
UnconstrainedMinimization ExampleConsider the problem of finding a set of values [x1, x2]that solves (2-1) To solve thistwo-dimensional problem, write an M-file that returns the function value. Then,invoke the unconstrained minimization routine fminunc. Step 1: Write an M-fileobjfun.m.function f = objfun(x)
f =exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
Step 2: Invokeone of the unconstrained optimization routines.x0 = [-1,1]; % Starting guess
options= optimset('LargeScale','off');
[x,fval,exitflag,output]= fminunc(@objfun,x0,options);
After40 function evaluations, this produ
fminuncFind a minimum of an unconstrained multivariable function where x is avector and f(x) is a function that returns a scalar. Syntaxx = fminunc(fun,x0)
x =fminunc(fun,x0,options)
[x,fval]= fminunc(...)
[x,fval,exitflag]= fminunc(...)
[x,fval,exitflag,output]= fminunc(...)
[x,fval,exitflag,output,grad]= fminunc(...)
[x,fval,exitflag,output,grad,hessian]= fminunc(...)
2、应用示例
求侧面积为常数6*52m2的体积最大的长方体体积。
设该长方体的长、宽、高分别为x1、x2和x3，据题意得到下面的数学模型：
编一个M文件optim25_2o.m，返回x处的函数值f。
function f = myfun(x)
f = -x(1) * x(2) * x(3);
由于约束条件是非线性等式约束，所以需要编写一个约束条件M文件opt25_2c.m：
function [c,ceq] = mycon(x)
ceq =x(2)x(3)+x(3)x(1)+x(1)x(2)-75
下一步给定初值，并调用优化过程(磁盘中M文件名为opt25_2.m)。
x0 = [4; 5; 6];
lb=zeros(3,1);
[x,fval,exitflag,output,lambda]=fmincon(@opt25_2o,x0,[],[],[],[],lb,[],@opt25_2c)
计算结果为：
Optimization terminated successfully:
Search direction less than2*options.TolX and
maximum constraint violation is less thanoptions.TolCon
Active Constraints:
1
x =
5.0000
5.0000
5.0000
fval =
-125.0000
exitflag =
1
output =
iterations: 7
funcCount: 38
stepsize: 1
algorithm: 'medium-scale: SQP,Quasi-Newton, line-search'
firstorderopt: []
cgiterations: []
lambda =
lower: [3x1 double]
upper: [3x1 double]
eqlin: [0x1 double]
eqnonlin: 2.5000
ineqlin: [0x1 double]
ineqnonlin: [0x1 double]
优化结果显示过程成功收敛，搜索方向小于两倍options.TolX，最大违约值小于options.TolCon，主动约束为1个。
问题的解为x(1)=x(2)=x(3)=5.0000m，最大体积为125.0000m3。exitflag=1，表示过程成功收敛于解x处。output输出变量显示了收敛过程中的迭代次数、目标函数计算次数、步长、算法等信息。lambda则包含模型信息。
实验四 机械优化设计实例
一、实验目的
1、能够针对实际优化设计及问题建立优化模型；
2、能够运用Matlab优化工具库对模型进行优化求解；
3、能结合实际和相关标准对优化结果进行处理。
二、实验条件
1.软件：MATLAB 7.0
2.硬件：配置良好的计算机
三、实验内容
某二级斜齿圆柱齿轮减速器，高速级输入功率
转速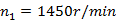
，总传动比i=31.5，齿轮宽度系数
，齿轮材料和热处理：大齿轮45号钢正火187～207HB，小齿轮45号钢调质228～255HB，工作寿命10年以上。要求按照总中心距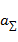
最小来确定齿轮传动方案。
解:(1)建立优化设计的数学模型
①设计变量：
将涉及总中心距a∑齿轮传动方案的6个独立参数作为设计变量
②目标函数：
减速器总中心距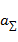最小为目标函数
③约束条件:含性能约束和边界约束
性能约束条件;
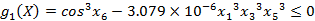高速级齿轮接触强度条件
低速级齿轮接触强度条件
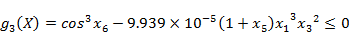高速级大齿轮弯曲强度条件
低速级大齿轮弯曲强度条件
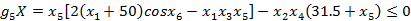大齿轮与轴不干涉条件
边界约束条件：
低速级齿轮副模数的下限和上限
高速级小齿轮齿数的下限和上限
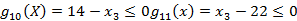高速级大齿轮齿数的下限和上限
低速级小齿轮齿数的下限和上限
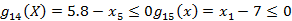高速级传动比的下限和上限
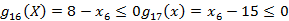齿轮副螺旋角的下限和上限
(2)编制优化设计的M文件
%两级斜齿轮减速器总中心距目标函数，文件名为：Jsqyh_f.m
function f=jsqyh_f(x);
hd=pi/180;
a1=x(1)*x(3)*(1+x(5));
a2=x(2)*x(4)*(1+31.5/x(5));
cb=2*cos(x(6)*hd);
f=(a1+a2)/cb;
%两级斜齿轮减速器优化设计的非线性不等式约束函数，文件名为：Jsqyh_g.m
function[g,ceq]=jsqyh_g(x);
hd=pi/180;
g(1)=cos(x(6)*hd)^3-3.079e-6*x(1)^3*x(3)^3*x(5);
g(2)=x(5)^2*cos(x(6)*hd)^3-1.701e-4*x(2)^3*x(4)^3;
g(3)=cos(x(6)*hd)^2-9.939e-5*(1+x(5))*x(1)^3*x(3)^2;
g(4)=x(5)^2.*cos(x(6)*hd)^2-1.076e-4*(31.5+x(5))*x(2)^3*x(4)^2;
g(5)=x(5)*(2*(x(1)+50)*cos(x(6)*hd)+x(1)*x(2)*x(3))-x(2)*x(4)*(31.5+x(5));
ceq=[];
[x,fval,exitflag,output, grad,hessian]=
fmincon(@fun,x0,A,b,Aeq,beq,Lb,Ub,’Nlc’,options,P1,P2…)
文件名为：eg9_6.m
x0=[2;4;18;20;6.4;10];%设计变量的初始值
lb=[2;3.5;14;16;5.8;8];%设计变量的下限
ub=[5;6;22;22;7;15];%设计变量的上限
[x,fn]=fmincon(@jsqyh_f,x0,[],[],[],[],lb,ub,@jsqyh_g);
disp ' ************两级斜齿轮传动中心距优化设计最优解*************'
fprintf(1,' 高速级齿轮副模数 Mn1=%3.4fmm\n',x(1))
fprintf(1,' 低速级齿轮副模数 Mn2=%3.4fmm\n',x(2))
fprintf(1,' 高速级小齿轮齿数 z1=%3.4fmm\n',x(3))
fprintf(1,' 低速级小齿轮齿数 z2=%3.4fmm\n',x(4))
fprintf(1,' 高速级齿轮副传动比 i1=%3.4fmm\n',x(5))
fprintf(1,' 齿轮副螺旋角 beta=%3.4fmm\n',x(6))
fprintf(1,' 减速器总中心距 a12=%3.4fmm\n',fn)
g=jsqyh_g(x); disp' ==========最优点的性能约束函数值=========='
fprintf(1,' 高速级齿轮副接触疲劳强度约束函数值 g1=%3.4fmm\n',g(1))
fprintf(1,' 低速级齿轮副接触疲劳强度约束函数值 g2=%3.4fmm\n',g(2))
fprintf(1,' 高速级大齿轮齿根弯曲强度约束函数值 g3=%3.4fmm\n',g(3))
fprintf(1,' 低速级大齿轮齿根弯曲强度约束函数值 g4=%3.4fmm\n',g(4))
fprintf(1,' 大齿轮顶圆与轴不干涉几何约束函数值 g5=%3.4fmm\n',g(5))
[x,fval,exitflag,output, grad,hessian]=
fmincon(@fun,x0,A,b,Aeq,beq,Lb,Ub,’Nlc’,options,P1,P2…)
(3) M文件运行结果及优化结果处理
************两级斜齿轮传动中心距优化设计最优解*************
高速级齿轮副模数 Mn1=2.0461mm→2mm
低速级齿轮副模数 Mn2=3.6059mm→4mm
高速级小齿轮齿数 z1=18.5156→19
低速级小齿轮齿数 z2=16.0000→16
高速级齿轮副传动比 i1=5.8000→5.8
齿轮副螺旋角 beta=8.0000→9.838mm ←
减速器总中心距 a12=317.4186mm→338.292→340mm↑
==========最优点的性能约束函数值==========
高速级齿轮副接触疲劳强度约束函数值 g1=0.0000mm
低速级齿轮副接触疲劳强度约束函数值 g2=0.0000mm
高速级大齿轮齿根弯曲强度约束函数值 g3=-1.0042mm
低速级大齿轮齿根弯曲强度约束函数值 g4=-15.1854mm
大齿轮顶圆与轴不干涉几何约束函数值 g5=-761.8043mm
